كم يكلّفنا الديّن في البنك؟
مسألة
مسألة 1
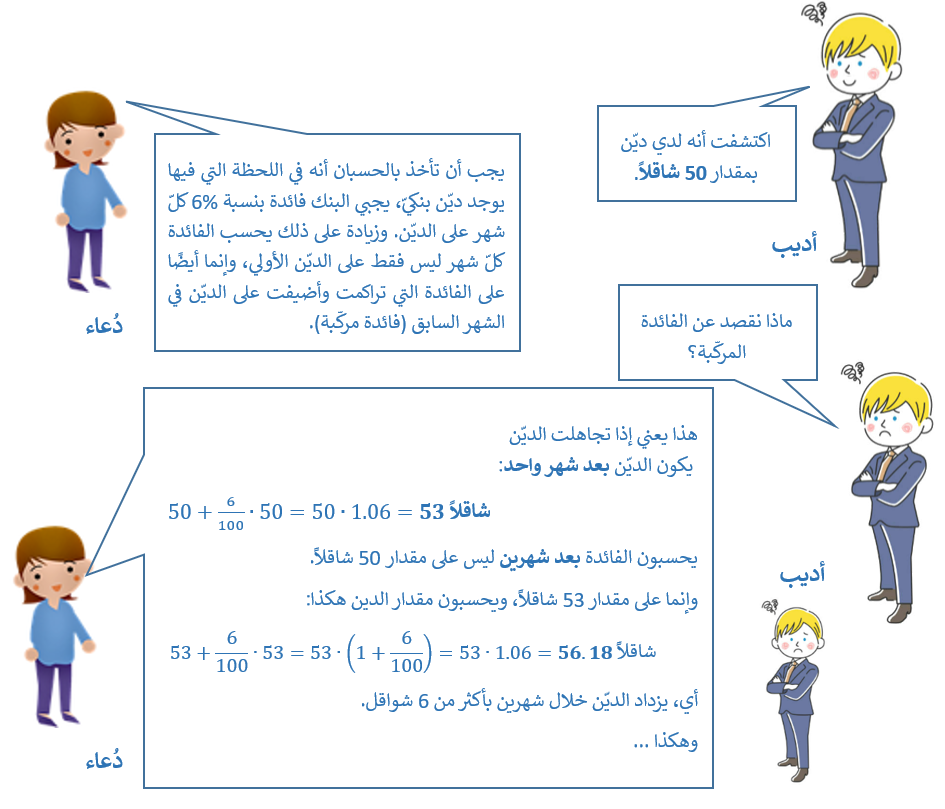
كي يفهم كيف يزداد مقدار الديّن مع مرّ الزمن، يحاول أديب ترتيب الحساب في جدول.
- ساعدوا أديب في إكمال الجدول: احسبوا مقدار الديّن بعد 4 أشهر.
اكتبوا تعبيرًا جبريًا يمثّل مقدار الديّن بعد \(n\) أشهر.
| شهر | مقدار الديّن في بداية الشهر | مقدار الديّن مع الفائدة | |
| حساب | مقدار الديّن في نهاية الشهر | ||
| 1 | 50 ₪ | \({50+\large\frac{6}{100}\normalsize\cdot50=50\cdot(1+\large\frac{6}{100}\normalsize)=50\cdot1.06}\) | 53 ₪ |
| 2 | 53 ₪ | \({50\cdot 1.06\cdot(1+\large\frac{6}{100}\normalsize)=50\cdot{1.06}^2}\) | 56.18 ₪ |
| 3 | 56.18 ₪ | \({50\cdot{1.06}^2\cdot(1+\large\frac{6}{100}\normalsize)=50\cdot{1.06}^3}\) | |
| 4 | |||
| \(n\) | |||
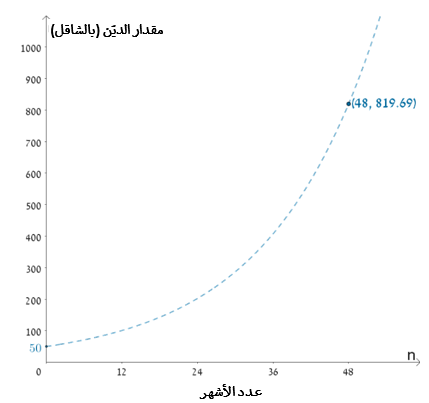
- أمامكم رسم بيانيّ يصف التغيّر في مقدار ديّن أديب وفقًا لعدد الأشهر.
تمعّنوا في الجدول وفي الخط البياني وأجيبوا عن الأسئلة التالية:
2 أ) هل يزداد مقدار الديّن بعد 5 أشهر بنسبة \(30\%\)؟
علّلوا.
2 ب) بعد كم من الزمن يضاعف مقدار الديّن الذي هو 50 شاقلاً نفسه مرتين؟
علّلوا ذلك بواسطة الرسم البياني
وافحصوا إجابتكم بواسطة التعويض في التعبير الجبري الذي سجّلتموه في البند 1.
2 ت) هل يُمكن أن يصبح مقدار الديّن أكثر من 1,000 شاقلاً؟
إذا نعم، قدّروا بعد كم من الزمن يحدث هذا.
مسألة 2
مقدار ديّن راني هو 1,000 شاقلاً. يجبي البنك فائدة بنسبة \(6\%\) كلّ شهر على الديّن.
- اكتبوا تعبيرً جبريًا يمثّل مقدار الديّن البنكيّ لراني بعد \(n\) أشهر.
- بكم مرة يكون مقدار الديّن لراني بعد 10 شهور أكبر من مقدار الدين لأديب؟
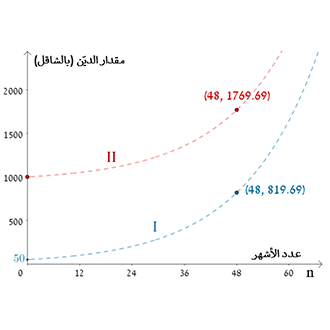
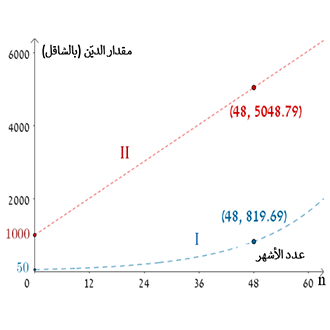
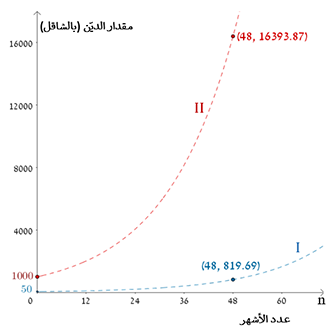
علّلوا. - أمامكم ثلاثة رسوم. يظهر في كلّ رسم سمان بيانيان.
الرسم البياني I يصف مقدار الدين لدى أديب.
في أي رسم يصف الرسم البياني II مقدار الديّن لدى راني؟ علّلوا.