כמה רחוק קו האופק - קירובים
תיאור סיטואציה
הגדרות יסוד
- קו האופק הוא קו ראיה אופקי שהוא בגובה העיניים של הצופה.
קו האופק עובר במקום המפגש הדמיוני הנצפה בין השמים לארץ או לים.
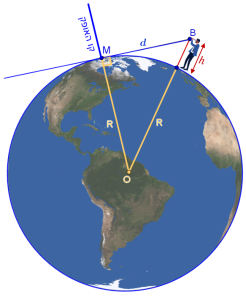
קיומו של קו האופק נובע מעקמומיות פני כדור הארץ, שבעטיה אין הצופה יכול לצפות בפני כדור הארץ מעבר לקו מסוים, הוא קו האופק. - נסמן בסרטוט (ראו תרשים משמאל):
את רדיוס כדור הארץ ב- R (נניח כי 6,371 ק"מ = R).
ונקודה על קו האופק M – זוהי נקודה שמבט הראיה שלנו מופנה אליה. - נגדיר את המשתנים ונסמן גם אותם על הסרטוט:
h – גובה עיניו של הצופה מעל פני כדור הארץ.
\(d (BM)\) – המרחק (בקו ישר) אל נקודה על קו האופק. - נתון כי המשולש OMB שנוצר הוא משולש ישר זווית (\({\measuredangle{M}=90^{\circ}}\))
*במציאות כדור הארץ אינו כדור מושלם.
(ניתן ללחוץ על כל תמונה וסרטוט ולהגדילם)
בעיה
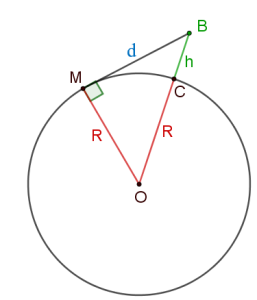
לפניכם סקיצה המתארת את הסיטואציה של מרחק צופה מקו האופק.
המעגל שמרכזו בנקודה O מייצג את כדור הארץ.
הנקודות O, B ו-C נמצאות על קו ישר אחד.
שימו לב: סקיצה משמעה סרטוט לא מדויק,
כך למשל, במציאות, רדיוס כדור הארץ (R)
גדול בהרבה יותר מגובה העיניים של הצופה (h).
- דנה נמצאת על שפת הים ומסתכלת על הסירה שמתרחקת מהחוף אל קו האופק.
נניח שגובה העיניים של דנה הינו כ- 1.5 מ',
1. כמה רחוק דנה יכולה לראות?
2. החל מאיזה מרחק (בערך) של סירה מהחוף, דנה כבר לא תוכל לראות אותה? - בכל סעיף נתון ערכו של h.
1. חשבו בקירוב את ערכי הביטויים הרשומים:
h R+h d 3 מטר 20 מטר 50 מטר משלכם: _______ מטר משלכם: _______ מטר
2. כתבו ביטוי אלגברי שמאפשר לחשב (בקירוב) את מרחקו של צופה אל קו האופק.
3. האם הביטוי \({\sqrt{2Rh}}\) הוא קירוב טוב לחישוב המרחק מקו האופק? נמקו תשובתכם.
\(\space\)
הידעתם? נוסחאות לחישוב מרחק קו האופק שימושיות למשל בקביעת גובהו של מגדל תצפית, או בקביעת המידה שבה על פריסקופ של צוללת לבלוט במים, כדי לצפות בכלי שיט עוינים.
