كرة سلة – قطع مكافئ
وصف وضعية
يرمي اللاعب في لعبة كرة السلة الكرة إلى السلة بهدف تسديدها في السلة.
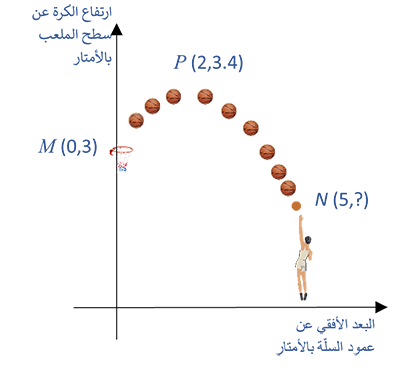
يُبيّن الرسم التوضيحي التالي مسار الكرة إلى السلة (أو إلى خارج السلة)، ومكان اللاعب ومكان السلة.
المسار الذي تمر به الكرة هو تقريبًا مسار قطع مكافئ.
نستعين في هذه المهمة بتمثيلات جبرية مختلفة للدالّة التربيعيّة كي تصف مسار الكرة وبذلك يمكن أن نعرف في أي حالات تدخل الكرة السلة وفي أيها لا تدخل.
مسألة
ارتفاع حلقة السلّة هو 3 م فوق سطح الملّعب.
اللاعب موجود على بُعد أفقي مقداره 5 م عن عمود السلّة.
يقفز اللاعب ويرمي الكرة.
تصل الكرة إلى أقصى ارتفاع 3.4 م،
وكانت على بُعد 2 م عن عمود السلّة.
دخلّة الكرة في السلّة.
نستعين في هيئة المحاور على الشكل التالي:
محور y يعبّر عن ارتفاع الكرة بالأمتار عن سطح الملّعب.
محور x يعبّر عن البُعد الأفقي بالأمتار بين الكرة وعمود السلّة.
أ. فسّروا معنى النقاط M, N و P.
ب. اختاروا التعبير الملائم لوصف مسار الكرة.
1. \(\space\space\space\space\)\(y=-0.1(x-2)^2+5\)
2. \(\space\space\space\space\)\(y=0.1(x-3)^2-3.4\)
3. \(\space\space\space\space\)\(y=-0.1(x-2)^2+3.4\)
4. \(\space\space\space\space\)\(y=x^2+2x+3\)
ت. جدوا على أي ارتفاع أطلق اللاعب الكرة.
(يمكن الضغط على الرسم وتكبيرها)
مسألة
يصف الشكل التالي مكان الكرة في أوقات مختلفة أثناء رميها إلى السلة.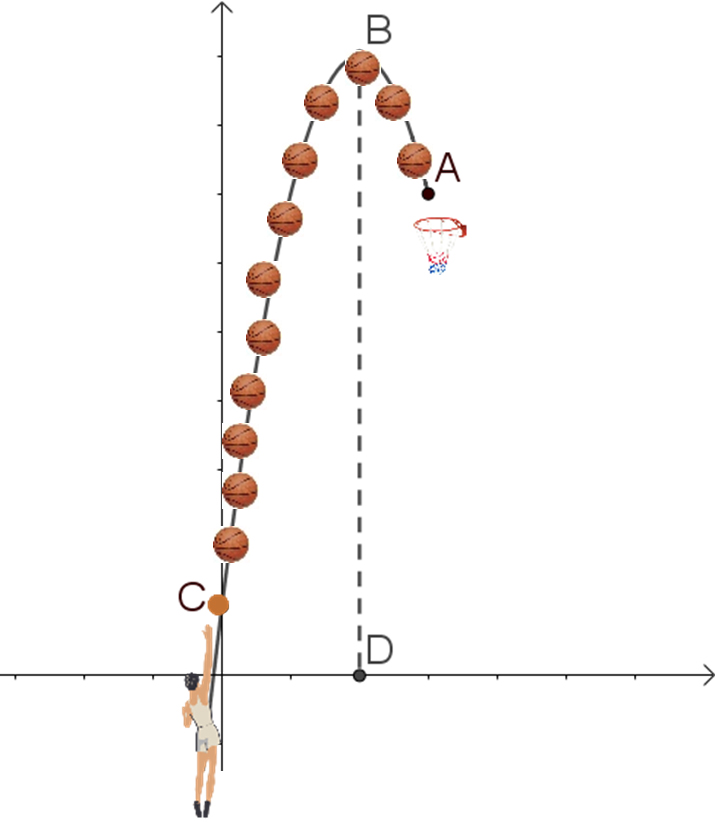
معطى أن اللاعب يُحرر الكرة في النقطة \(C(0,2)\) والسلة موجودة في النقطة \(A(6,14)\).
الارتفاع الأعلى الذي تصل إليه الكرة هو 18 وحدة طول.
فيما يلي تعابير جبرية.
اختاروا التعابير الملائمة لوصف مسار الكرة.
- \(y=-x^2+8x+18 \space\space\space\)
\(\space\) - \(y=-(x-6)(x-14) \space\space\space\)
\(\space\) - \(y=-(x-4)^2+18 \space\space\space\)
\(\space\) - \(y=-(x-6)^2+14 \space\space\space\)
\(\space\) - \(y=-x^2+8x+2 \space\space\space\)
يمكن الاستعانة بالتطبيق.
(يمكن الضغط على الرسم وتكبيرها)
- لائموا لكل واحد من التعابير التالية, الرسم البياني الملائم لوصف مسار الكرة.
- أشيروا بـ V من خانة الاختيار وافحصوا هل تقع النقاط المعطاة على المسار الذي اخترتموه.
