כמה רחוק קו האופק - גרפים
תיאור סיטואציה
הגדרות יסוד
- קו האופק הוא קו ראיה אופקי שהוא בגובה העיניים של הצופה.
קו האופק עובר במקום המפגש הדמיוני הנצפה בין השמים לארץ או לים.
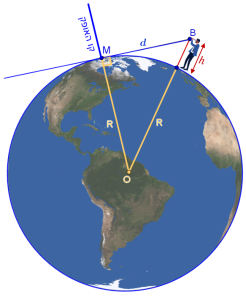
קיומו של קו האופק נובע מעקמומיות פני כדור הארץ, שבעטיה אין הצופה יכול לצפות בפני כדור הארץ מעבר לקו מסוים, הוא קו האופק. - נסמן בסרטוט (ראו תרשים משמאל):
את רדיוס כדור הארץ ב- R (נניח כי 6,371 ק"מ = R).
ונקודה על קו האופק M – זוהי נקודה שמבט הראיה שלנו מופנה אליה. - נגדיר את המשתנים ונסמן גם אותם על הסרטוט:
h – גובה עיניו של הצופה מעל פני כדור הארץ.
\(d (BM)\) – המרחק (בקו ישר) אל נקודה על קו האופק. - נתון כי המשולש OMB שנוצר הוא משולש ישר זווית (\({\measuredangle{M}=90^{\circ}}\))
*במציאות כדור הארץ אינו כדור מושלם.
בעיה
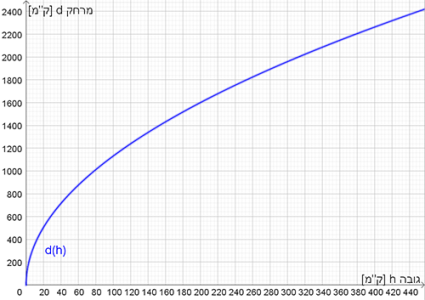
לפניכם גרף של הפונקציה \(d(h)\) המתארת את מרחקו \((d)\) (בק"מ) של צופה אל קו האופק,
כתלות בגובה העין \((h)\) (בק"מ) של הצופה מעל פני כדור הארץ.
- תחנת חלל נמצאת בגובה של כ-400 קילומטר מעל פני כדור הארץ.
אסטרונאוט בתחנה מסתכל לעבר כדור הארץ. באיזה מרחק ממנו נראה קו האופק?
הסבירו כיצד קבעתם וסמנו נקודה מתאימה על הגרף. - בשנת 2014 אלן יוסטס, סגן נשיא בחברת גוגל, קבע את שיא העולם לנפילה חופשית מגובה של כ-41 ק"מ.
1. חשבו מה היה המרחק של אלן יוסטוס אל קו האופק.
2. סמנו נקודה מתאימה על גרף הפונקציה.
3. בכמה רחוק יותר (בערך) המרחק שרואה האסטרונאוט הנמצא בתחנת החלל, מאשר המרחק שרואה אלן יוסטס בתחילת הנפילה? - 1. אפיינו את קצב ההישתנות של הפונקציה \(d(h)\).
2. תארו לפחות שתי תכונות שונות נוספות של הפונקציה \(d(h)\) בהסתמך על הגרף.
כיצד תכונות אלה באות לידי ביטוי בחיי היומיום?
\(\space\)
הידעתם? נוסחאות לחישוב מרחק קו האופק שימושיות למשל בקביעת גובהו של מגדל תצפית, או בקביעת המידה שבה על פריסקופ של צוללת לבלוט במים, כדי לצפות בכלי שיט עוינים.