גשר שער הזהב
תיאור סיטואציה
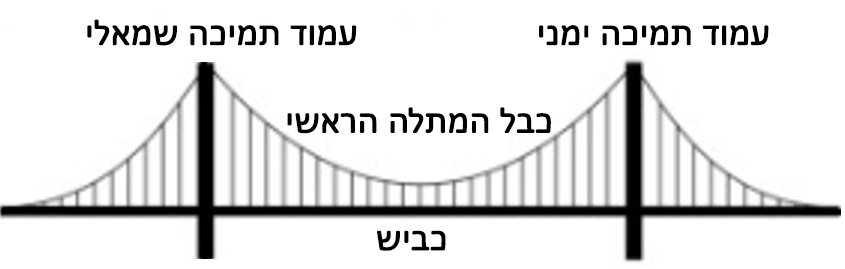
חלק מהגשרים הארוכים בעולם, מורכבים מכבלים התלויים בצורה של קשתות פרבוליות בין עמודי תמיכה. הצורה הפרבולית של הכבלים תומכת בגשר.
הכבלים הפרבוליים מחלקים באופן שווה את משקל הגשר, בין עמודי תמיכה זהים, שאליהם הם מחוברים ומאפשרים לשאת את המשקל של מאות כלי רכב העוברים על הגשר.
אחד מהגשרים התלויים המפורסמים הוא גשר שער הזהב בסן פרנסיסקו, קליפורניה.
בעיה
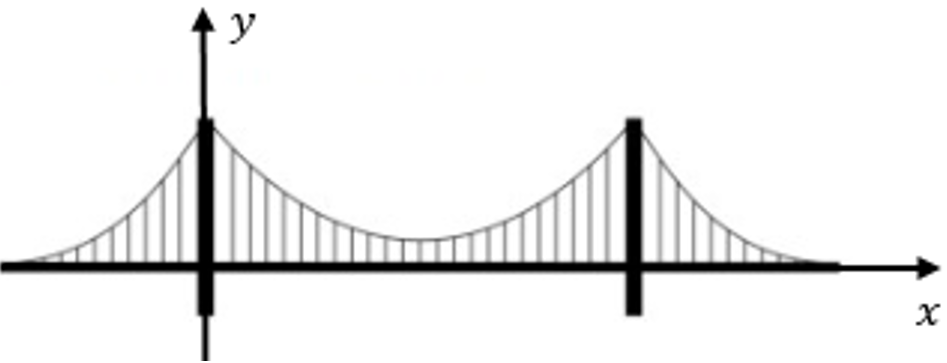
נשרטט מערכת צירים באופן הבא:
ציר ה- x עובר על מפלס הגשר (בהנחה שהכביש בקטע שבין שני העמודים הוא אופקי),
וציר ה- y עובר על עמוד התמיכה השמאלי (ראו סרטוט).
כבל המתלה הראשי הוא בצורת פרבולה.
הפונקציה הקובעת את גובה המתלה של הגשר היא \(y=\Large\frac{19}{51,200}\normalsize x^2-\Large\frac{19}{40}\normalsize x+155\),
כאשר x ו-y נמדדים במטרים.
- מה מבטאים במציאות השיעורים של נקודה \((320, 41)\) שעל גרף הפונקציה?
- מהו הגובה מעל הכביש של עמודי התמיכה שעליהם תלוי הכבל?
- מהו המרחק הקצר ביותר מהכבל לכביש?
- מהו המרחק בין שני עמודי התמיכה?
(ניתן ללחוץ על כל תמונה ולהגדילה)
